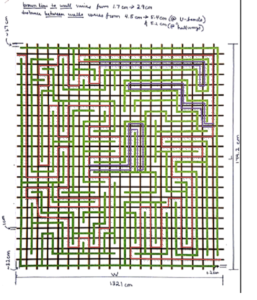
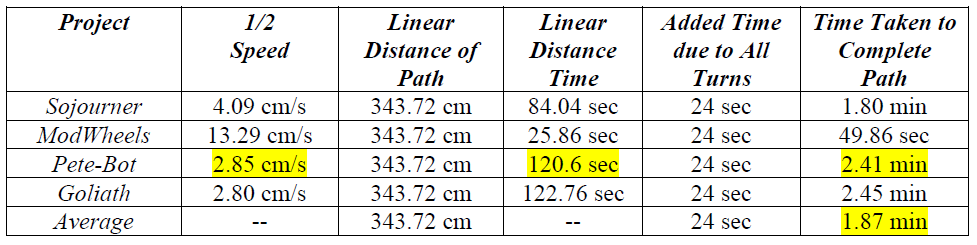
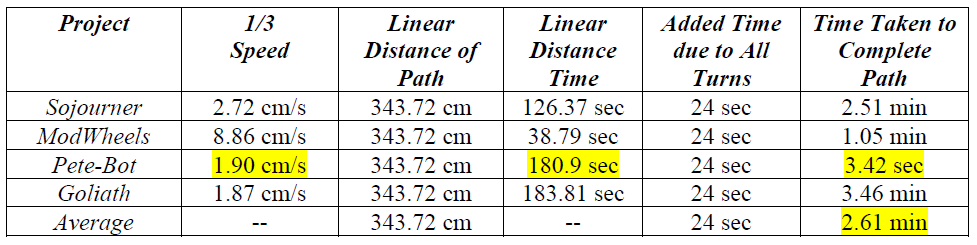
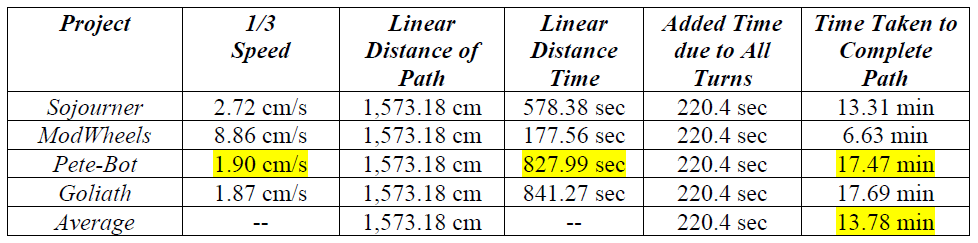
Robot Avoidance Pseudocode

/in /by

Written  by Elizabeth Nguyen (Project Manager)

Description: (updated on 11/19/17)

The robot avoidance code is a program that will allow robots to avoid each other under various cases after a robot detects another. There currently two parts: (1) Robot Detection (written by John Campo) and (2) Robot Avoidance. The psuedocode outlines a potential algorithm that can be implemented for the Robot Avoidance code.

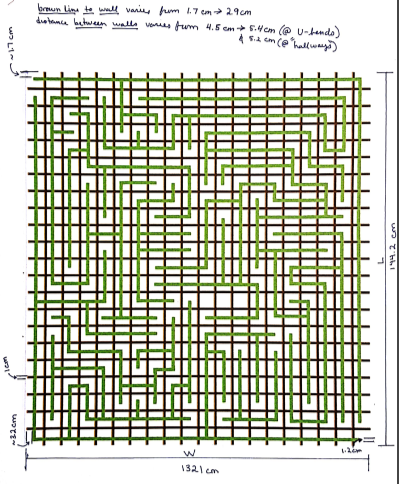
Currently, this task is linked to Rules of the Maze.

Constraints

Due to the complexity of this algorithm, the psuedocode only assumes that two robots may collide with each other. Later on, it can be built upon in the case that three robots may collide with each other or even four.

Because of this constraint and based on the Rules of the Maze, it can be assumed that North- and East-facing robots will be not need to stray off their paths when “colliding” with a robot. South- and West-facing robots however will have to carry the burden to move away to allow the respective North- and East-facing robot to continue forward.

Also, regardless of direction, any robot located in an intersection will automatically carry the burden of moving away.

Pseudocode

Avoidance
   Identify direction
   Find out which room robot is in (Subroutine - WhichRoom)
   Get location from WhichRoom
   If the robot is in an intersection
      Save current location (this location can be passed to another subroutine where it can return to its original path)
      Move away (Subroutine - MoveAway)
      Return to its original path
      Continue the maze path
   Else (this is where direction will matter)
      If the robot is facing North OR East
         Check if a robot is in front of it (Subroutine - CheckAgain)
         Wait for 30 seconds (to ensure that the robot facing South moves away)
         Continue the maze path
      If the robot is facing South OR West
         CheckAgain
         Save current location (this location can be passed to another subroutine where it can return to its original path)
         Move away by backing into the nearest corner or intersection
         Return to its original path
         Continue the maze path
         
WhichRoom
   Determine location
   Return location to Avoidance subroutine

MoveAway
   Determine path to take
   Move backwards
   CheckAgain
   Return to Avoidance subroutine

CheckAgain
   Run Robot Detection Code
   If robot is detected
      Return to Avoidance subroutine
   Else
      Resume original path

Other Notes

Despite the current pseudocode possessing the parts of if-else statements, I believe it would be better to implement a finite state machine for avoidance. There also could be complications with determining how a robot can return to its original path after moving away. Interrupts may need to be utilized since there are many moments where a robot may not need to complete the avoidance subroutine.

Goliath Fall 2017 – Gyro Test & Power Usage

/in , /by

The measured results are at the board level of the required voltage and current draw of the Gyro sensor. The voltage was able to measure with a simple multimeter but the current draw was in the single digit milliamps requiring us to use a more precise multimeter. We supplementally added a demo of how the […]

Read more

Pete-Bot Custom Command and Telemetry

/in /by

Written by Elizabeth Nguyen (Project Manager)

Description:

A short list of custom commands and custom telemetry are defined in preparation for the EE 400D Fall 2017 Mission.

Custom Commands

  • Adjustable Speed Commands – Allows the robot to run at a specific set speed
    • Option for slowest speed
    • Option for medium speed
    • Option for fastest speed
    • On/Off for adjustable speed
  • Emergency On/Off Command – in the case that the robot is incapable of operating in Phase 2b
    • This is to avoid damage to the robot and other robots
    • Avoids the need for anyone to step into the maze and pick up the robot to disable it

Custom Telemetry

  • Display of Phase the robot is operating in
  • Robot detected
    • State that the robot is in during robot avoidance

Goliath Fall 2017 – Recommended Custom Telemetry & Custom Commands

/in , /by

The purpose of this document is to define telemetry visuals and custom commands required in Arxterra to control the Goliath during the mission. These definitions will be used in the software design on both the application side and the internal operating code of the Goliath. These commands may be subject to change if some are not possible […]

Read more

Mission Definition

/in /by

Written by Elizabeth Nguyen (Project Manager)

Table of Contents

Objective:

The total time for each phase of the mission set is determined in order to ensure there is enough time allocated for the entire mission set to be completed in 120 min.

This document entails the breakdown of the mission set and how much time is split for each phase based on the maximum speed of each robot as provided in Mission Duration at Maximum Speed.

Phases:

  • Phase 1 – Record
  • Phase 2a – Individual Playback
  • Phase 2b – 4 Robots, 1 Maze
  • Phase 2c – Individual Playback (Pre-defined)*

* Phase 2c is optional and based on the success of Phase 2a

Robot Order: (from fastest to slowest)*

  • Pete-Bot** – 6 min.
  • ModWheels** – 7 min.
  • Sojourner** – 14 min.
  • Goliath – 18 min.

* All times have been rounded up
** Assumes no load

Speeds & Path Durations used:

Path durations were calculated and documented by Railan Oviedo. There are two documents where one addresses the path duration at maximum speed and another at minimum speed.

The bolded texts indicate which numbers I used to determine allocated time.

Types of Path Scenarios:

  • Shortest Path Scenario
  • Average Path Scenario

Speeds:

  • Half Speed – Min Speed
  • Half Speed – Max Speed
  • One-Third Speed – Min Speed
  • One-Third Speed – Max Speed

One-third speed was chosen (and suggested by Mark Huffman) to account for potential decrease in time due to added weight (since all but one robot have provided speeds under no load conditions). Although half-speed would be better to use for worst-case scenarios, it may not be as reasonable either. Also, average path durations were chosen to determine total time allocations at worst.

Breakdown of Mission Set:

  1. Phase 1 – Record
    1. Average Path Scenario at One-Third Speed (Max Speed)
      1. Total Time: 54 min.
        1. Path completion: 45 min.
        2. Rotation: 3 min. x 3 rotations = 9 min.
    2. Concluded Total Time: 60 min.
      1. Rounded up in the case that rotations are not 3 min. each or that some robots end up not performing up to speed due to added weight.
  2. Phase 2a – Individual Playback
    1. Concluded Total Time: 60 min.
      1. Considering that this phase is to test if the robot has properly recorded the maze, it can be assumed that the amount of time it takes to individually playback each robot is the same as Phase 1.
      2. Assuming that there is only one maze available, this means that the amount of time to complete the mission set has been allocated to both Phase 1 and Phase 2a.
    2. Alternative: (has been approved by Hill)
      1. If two mazes are available, then Phase 1 and Phase 2a can occur simultaneously.
      2. Once one robot completes Phase 1, it may proceed to Phase 2a on the second maze.
      3. This would allow Phase 1 || Phase 2a to be completed in 60 min.
  3. Phase 2b – 4 Robots, 1 Maze
    1. Concluded Total Time: 20 min.
      1. Total time is based on the time it takes for the slowest robot (Goliath) to playback its recorded path. At worst, that is 18 minutes; however, including factors such as robots potentially detecting each other and having to avoid each other, 2 minutes has been added in.
        1. Note: At this time, it is unknown how long it will take a robot to execute the Robot Avoidance Code and recover from its detour.
        2. If it takes even longer for a robot to avoid another, maybe a rule should be made where if a robot takes three attempts to correct itself and fails, then it fails Phase 2b and should be removed from the maze.
  4. Phase 2c – Individual Playback with Pre-Defined Maze
    1. This Phase only occurs if a robot fails to complete Phase 2a.
    2. Best Case: 0 min.
      1. All four robots must complete Phase 2a successfully.
    3. Worst Case: 60 min.
      1. All four robots fail to complete Phase 2a.
    4. Duration based on the number of robots at best and at worst in minutes:
      [Mission Set Table]
    5. Disassembly & Reassembly
      1. Total Time: 20 min.
        1. Based on Natalie Arevalo’s conclusion
          1. Disassembly: 10 min.
          2. Reassembly: 10 min.

Scenarios:

  1. Best Case Scenario – 100 min.
    1. Reasoning:
      1. Phase 2c is not required
      2. Phase 1 || Phase 2a (two mazes are required)
    2. Breakdown:
      1. Phase 1 || Phase 2a – 60 min.
      2. Phase 2b – 20 min.
      3. Phase 2c – 0 min. (if all robots succeed in Phase 2a or if Phase 2c is not included)
    3. Disassembly & Reassembly – 20 min.
    4. This scenario has been selected for the demonstration date on December 13, 2017.
  2. Worst Case Scenario – 160 min.
    1. Reasoning:
      1. Phase 2c is not required
      2. Phase 1 and Phase 2a occur separately
    2. Breakdown:
      1. Phase 1 – 60 min.
      2. Phase 2a – 60 min.
      3. Phase 2b – 20 min.
      4. Phase 2c – 0 min.
    3. Disassembly & Reassembly – 20 min.
  3. Absolute Worst Case Scenario – 220 min.
    1. Reasoning:
      1. Phase 2c occurs with all four robots
      2. Phase 1 and Phase 2a occur separately
    2. Breakdown:
      1. Phase 1 – 60 min.
      2. Phase 2a – 60 min.
      3. Phase 2b – 20 min.
      4. Phase 2c – 60 min.
  4. Disassembly & Reassembly – 20 min.

Mission Duration at Maximum Speed

/in /by

Descriptions, Calculations, and Images by Railan Oviedo (Manufacturing)

Description:

In order to calculate the mission duration, multiple paths were created and averaged in order to have a rough estimate on the time length. These paths were made intentionally long in distance so as to simulate worst-case scenario situations. Based on the given speeds of the robot*, the longest time to complete the average calculated path is 17.69 minutes (Goliath). Further calculations were made for the shortest possible path, and differences in time based on the average speed used by the robot (Either Half-Speed or One-Third Speed).

*P-Bot and ModWheels speeds were calculated assuming the motors are running are 5 V

Updated on 11/17/2017.

Methods of Calculation

First, the shortest path possible will be calculated in order to determine the best case scenario mission duration. Then, 6 long maze paths—which will start and end at the entrance and exit of the maze—will be created (4 of which will be off-shoots of the first 2) and their distance will be averaged in order to simulate any given run through the maze.

To calculate the time that a particular robot will take to navigate the averaged path, their provided speed will be reduced by a third—and another scenario with the speed reduced by a half—due to the fact that it will likely move slowly to maintain contact with the colored line. Furthermore, for every turn, an extra 2 seconds will be added to account for the action; and for every U-turn, an extra 6 seconds will be added to account for the action.

Robot Speeds:

All robot speeds besides Goliath are at no-load based off of calculations from the wheel diameter and the RPM of the robot’s given motor.

Table (1) – Robot Speeds

* These speeds assume a constant 5V supply to the motors, thus resulting in an RPm of 64

** Goliath’s speed is provided under their estimated weight conditions

Maze Calculations

Reference for Maze Dimensions by Zachary de Bruyn

Image of Maze with Dimensions

One strip of brown is approximately 6.61 cm (132.1 cm/20 cm).*

*U-Turns will not be counted as a strip traveled and are only factored into the aformentioned 6 sec./U-Turn condition.

Shortest Possible Path

  • Total Number of Turns: 12
    • Time to be added: 12 * 2 sec. = 24 sec.
  • Total brown strips covered: 52
    • Linear distance: 52 * 6.61 cm = 343.72 cm = 3.4372 m.

Longest Path Option 1a

  • Total Number of Turns: 62
    • Time to be Added: 62 * 2 sec. = 124 sec.
  • Total brown strips covered: 170
    • Linear Distance: 170 * 6.61 cm = 1,123.7 cm = 11.24 m.

Longest Path Option 1b

  • Total Number of Non U-Turns: 62 + 8 + 8 = 78; Total Number of U-Turns: 3
    • Time to be Added due to Non U-Turns: 78 * 2 sec. = 156 sec.
    • Time to be Added due to U-Turns: 3 * 6 sec. = 18 sec.
  • Total brown strips covered: 170 + 28 + 10 + 6 = 214
    • Linear Distance: 214 * 6.61 cm. = 1,414.54 cm = 14.15 m.

Longest Path Option 1c

  • Total Number of Non U-Turns: 62 + 14 + 8 + 12 = 96; Total Number of U-Turns: 5
    • Time to be Added due to Non U-Turns: 96 * 2 sec. = 192 sec.
    • Time to be Added due to U-Turns: 5 * 6 sec. = 30 sec.
  • Total brown strips covered: 170 + 26 + 30 + 30 = 256
    • Linear Distance: 256 * 6.61 cm. = 1,692.16 cm. = 16.92 m.

Longest Path Option 2a

  • Total Number of Turns: 80
    • Time to be Added: 80 * 2 sec. = 160 sec.
  • Total brown strips covered: 208
    • Linear Distance: 208 * 6.61 cm. = 1,374.88 cm. = 13.75 m.

Longest Path Option 2b

  • Total Number of Non U-Turns: 80 + 2 + 10 + 8 = 100; Total Number of U-Turns: 3
    • Time to be Added due to Non U-Turns: 100 * 2 sec. = 200 sec.
    • Time to be Added due to U-Turns: 3 * 6 sec. = 18 sec.
  • Total brown strips covered: 208 + 24 + 24 + 26 = 282
    • Linear Distance: 282 * 6.61 cm. = 1,864.02 cm. = 18.64 m.

Long Path Option 2c

  • Total Number of Non U-Turns: 80 + 8 + 6 + 4 = 98; Total Number of U-Turns: 3
    • Time to be Added due to Non U-Turns: 98 * 2 sec. = 186 sec.
    • Time to be Added due to U-Turns: 3 * 6 sec. = 18 sec.
  • Total brown strips covered: 208 + 28 + 40 + 22 = 298
    • Linear Distance: 298 * 6.61 cm. = 1,969.78 cm. = 19.70 m.

Results:

After calculating all the numerical values, the following tables have been compiled.

Table (2) – Total Linear Distance, Added Time, and Average Values

Table (3) – Shortest Mission Duration at Half-Speed (Shortest Path Scenario)

Table (4) – Shortest Mission Duration at One-Third Speed (Shortest Path Scenario)

Table (5) – Average Mission Duration at One-Third Speed (Average Path Scenario)

Final Notes

These estimations do not factor into account the time it would take to navigate a path that starts at a random point in the maze. However, since the created paths are incredibly large—in order to simulate a worst-case scenario—it is safe to assume that, in practice, the total time taken to navigate any given path will be less than the calculated values. This also assumes that the processes of turning or U-turning do not require considerably more amount of time to execute than originally assumed.

Maze Dimensions

/in /by

Written by Elizabeth Nguyen (Project Manager)

Measurements taken by Zachary de Bruyn (Electronics & Control)

Dimensions:

  • Total width: 132.1 cm.
  • Total length: 144.2 cm.
  • Brown line to wall (green line) varies from 1.7 cm to 2.9 cm.
  • Distance between walls varies:
    • 4.5 cm to 5.4 cm @ the U-bends
    • 4.5 cm to 5.2 cm @ hallways
  • Thickness of horizontal brown lines is 1 cm.
  • Thickness of vertical brown lines is 1.2 cm.

Scan of Maze with Dimensions