Servo Motor Trade-Off Study With Torque Analysis

By: Parker Anderson (torque calculations) & Brandon Serna (Servo Tradeoff)

Our mechanical arm requires servos that are capable of providing enough torque to lift the arm, extend, and lift a Jenga-block with a claw that is also operated by a servo.  Because our initial V1 arm utilizes SG90 servos, we had to keep the dimensions of the servo in mind as we compared and chose our servos for later iterations of the arm.

Servo minimum requirements:

  • Weight: < 20 grams
    • Servo weight must not hinder the arm and Goliath operations.
  • Torque < 1.9Kg/cm
    • Servos must be able to operate at the desired torque as per the torque calculations, which include lifting the arm with a Jenga Block.
  • Dimensions: No bigger than 30mm x 20mm x 30mm
    • Servos must fit into the existing dimensions as the V1 arm design as to not further increase the complexity of the mechanical design.

Servo Motor Trade-Off Study

Name Model Weight
(Grams)		 Speed
(sec/degree)		 Torque
(kg/cm)		 Dimensions
(mm)		 Requirements
TowerPro MG995 55 0.2/60 9.4@ 4.8V 40.7×19.7×42.9 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
TowerPro SG90 14.7 0.12/60 1.6@ 4.8V 22x12x23 ✓ WEIGHT

✗ TORQUE

✓ DIMENSIONS
Annimos DS3218MG 60 0.12/60 21.5@ 6.8V 40x20x40.5 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
SunFounder N/A 55 0.12/60 12@ 4.8V 54.1x20x44.3 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
TowerPro SG5010 39 0.2/60 5.5@ 5V 40x20x38 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
Hobbypark HDR315M 15k 0.14/60 13.5@ 5V 40x20x40.5 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
HiTech HS-422 45.5 0.16/60 3.3@ 4.8V 40.39x19x56
x36.58		 ✗ WEIGHT

✓ TORQUE

✗ DIMENSIONS
TowerPro MG90S 14 0.11/60 2.2@ 4.8V 23.1x12x2x29 ✓ WEIGHT

✓ TORQUE

✓ DIMENSIONS

After tabulating various motors and their different characteristics, along with the desired requirements, we came to the conclusion that the TowerPro MG90S was the best candidate for the claw and arm mechanisms respectively.  Had we progressed our design further and printed the arm and claw out of acrylic material rather than wood, it is possible that servos with slightly higher torque may need to implemented due to being more dense. 

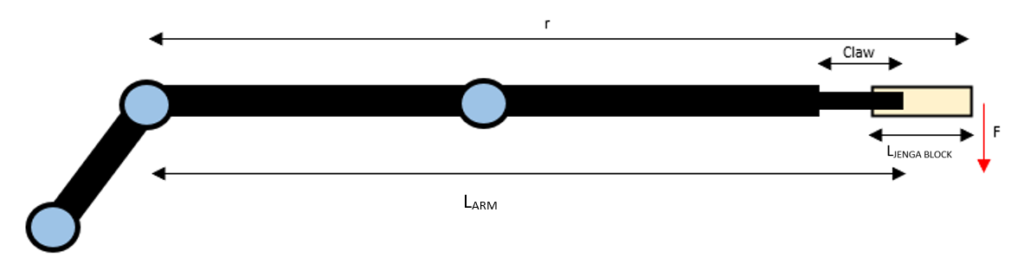
The mechanical role of this project requires a torque calculation for what the arm servos can handle. We started this process by looking back into physics knowledge of center of mass, torque, and force concepts and applying them to our arm.

We started the analysis by using our measurements of the arm’s mass, a Jenga block’s mass, our arms fully straightened length, and the Jenga blocks length. Using those masses in kilograms we could calculate the gravitational force (weight in Newtons). After calculating the force in Newtons we could multiply the force with the length of the arm and block.

We also had to find the center of mass by using the sum of torques in one direction and setting them equal to the sum of torques in the opposite directions. Summing up the arm torque and Jenga block torque and dividing it by the force of the arm and the force of the Jenga block we could find the distance from my chosen pivot point to find the center of mass. Using that distance to the center of mass we can multiply that by the total force of the arm and Jenga block to find that torque. We will include pictures of derivations below so it can be viewed in a more clear and concise way. From the calculations being compared to the servo torque limits our arm will be able to pick up the Jenga block with ease.

ARM MODEL

Figure 1. Arm Model

Figure 2. Torque Equation Set 1

FREE BODY DIAGRAM

Figure 3. Free Body Diagram

Figure 4. Torque Equation Set 2

CENTER OF MASS

Figure 5. Torque Equation Set 3

TOTAL TORQUE

Figure 6. Torque Equation Set 4

SERVO TORQUE

Figure 7. Torque Equation Set 5

Figure 8. V2 and V3 arm torque compared to MG90S servo torque

Our MG90S servo would work decently with our V2 arm while holding a Jenga Block. If we’re able to proceed to our V3 arm, we would probably want to find another servo with a better torque rating.