Mod Wheels Generation #3 Loop/Course Mission Analysis and Calculations
Mod Wheels/Spring/2020
Spring 2020: Mod Wheels Loop/Design Analysis and Calculations
Author: Frank Torres (Design & Manufacturing). Israel
Table of Contents
Loop-the-Loop
Completing the loop was our main focus and I knowing the dimensions of V2’s chassis that was to be created would be significant in determining the minimum diameter sized loop and velocity needed for Mod Wheels complete it.
Radius vs Speed Needed to Complete Loop
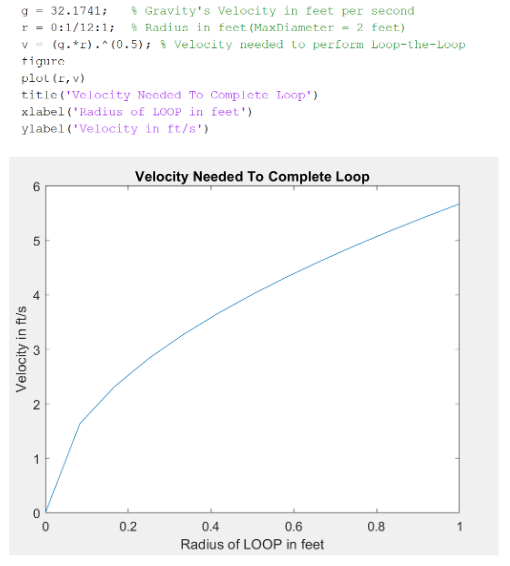
After thorough research I found an equation that’s proportional to the radius and velocity needed to complete it shown in Figure.2.
Figure.2 – Velocity needed to complete loop equation
Knowing the equation, I used MATLAB to code and output the velocity and radius needed to complete a loop with the maximum radius of one foot displayed in Figure.3.
Figure.3 – MATLAB’s output given the equation
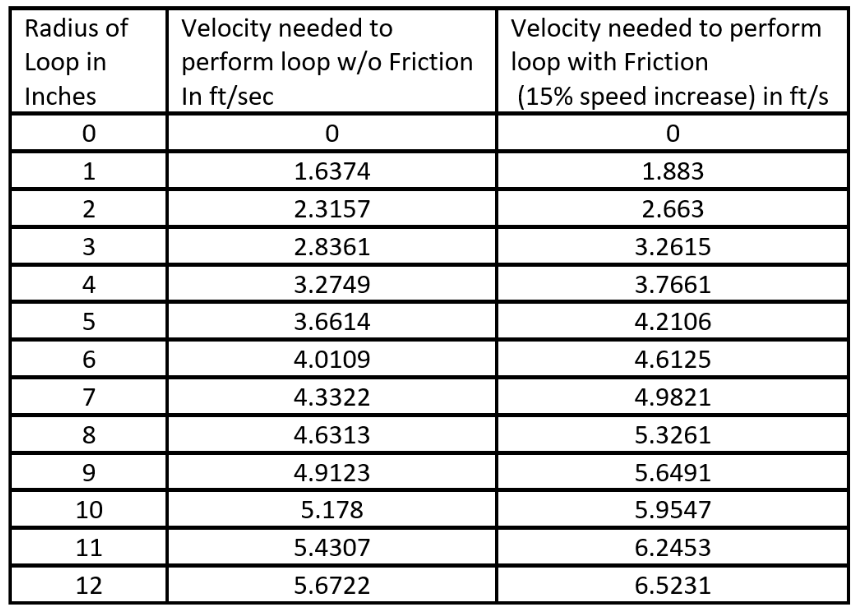
Figure.4 then shows a table showing the velocity needed to complete the loop with respect to velocity.
Figure.4 – “Radius vs Velocity Need to Complete Loop” table
Course Design
For the course design we went with an open course including a loop and ramp. We did this due to the mod wheels turbo boost feature that allows it to suddenly increase speed making it hard to control in a closed course. without boost our car goes about 2.3ft/sec and takes about 2 minutes to charge. so it can travel up to 276 feet before it would even get a full charge. Also with boost active will last about 40 seconds and it can read a distance of 232 feet in one boost but most of this energy will wasted in attempt of the loop.
Conclusion
The radius and velocity needed to complete the loop was solved through an equation I found online. I used the equation in MATLAB to output the velocities needed if the radius of the loop went from 0-12in. With this data the team decided we would try a radius of 6in which would require us to have a minimum speed of 4.6125 ft/s to complete the loop
References/Resources
- https://www.dummies.com/education/science/physics/calculate-the-velocity-necessary-to-counteract-gravity-in-a-loop/